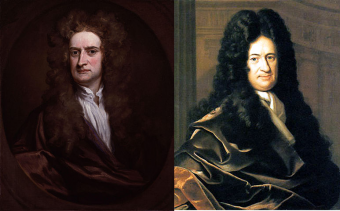Calculus involves the study of limits. By the time they were done arguing about who had invented it, Isaac Newton and G. W. Leibniz had probably both reached their limit as well.

Science has seen a number of simultaneous discoveries. Michael Faraday and Joseph Henry independently discovered electromagnetic induction. Charles Darwin and Alfred Russel Wallace both hit upon the idea of natural selection. None of these coincidences, however, snowballed into an argument as ugly as the one that developed between Isaac Newton and Gottfried Wilhelm Leibniz over the invention of calculus.

THE ROOTS OF THE PROBLEM

Newton didn’t like to publish. He was one of the most innovative thinkers of his day, making breakthroughs in physics and mathematics that inspired vast new fields of study, but he never felt his work was quite ready to go to the printer—he always wanted to make changes or write another draft. Because of his hesitation, he didn’t get any of his work on calculus into print until 1704. Leibniz, a leading philosopher and mathematician, beat him to the punch by publishing a brief summary in the Leipzig periodical Acta Eruditorum in October 1684.

However, Newton had planted a few clues about his pioneering work in calculus. Starting in 1676, he circulated unfinished papers privately among his friends that hinted at calculus concepts. Two letters about calculus topics even went to Leibniz that year. But his first public hint was in his greatest work published in his lifetime, Principia Mathematica (1687), when Newton tossed in a theorem about differentiation, one of the basic operations of calculus.

In fact, in a note on this theorem, Newton revealed a secret message from one of his letters to Leibniz. In this letter, Newton had concealed the meaning of a sentence by jumbling all of its letters. The secret message was “Given any equation involving flowing quantities, to find the fluxions, and vice-versa.” When Newton wrote the letter, he had wanted to establish proof that he had discovered a fundamental theorem of calculus, but he didn’t want Leibniz to know it, so he scrambled all the letters of it together. That way, he could point to it later for proof, but Leibniz couldn’t steal it.

Never mind that no one knew what “fluxions” were, since Newton had invented the word. Also never mind that Leibniz couldn’t read the message because the letters were all out of order. Newton’s point was that he had staked a claim to the concepts in 1676, even though the secret message didn’t really communicate anything to Leibniz…or anyone else.

THE TROUBLE MULTIPLIES

At first, Newton and Leibniz were both inclined to give the other credit for being an independent discoverer. It was their friends who really turned them against each other. It started in 1696 when a friend of Leibniz published a challenge problem that required calculus in the Leipzig Acta hoping that Newton wouldn’t be able to solve it, thus proving that Newton had stolen calculus from Leibniz. Newton, of course, solved the problem easily, as did Leibniz. But Leibniz, who was a careless worker, wrote an article about the problem that seemed (to Newton’s friends) to imply that Leibniz had invented calculus and that Newton was Leibniz’s student.

DO YOU COPY?

A friend of Newton’s then angrily wrote an analysis of the challenge problem in which he indirectly accused Leibniz of plagiarism:

As to whether Leibniz, [calculus’s] second inventor, borrowed anything from him, I prefer to let those judge who have seen Newton’s letters and other manuscript papers, not myself.

This referred to the letter Newton sent Leibniz with the inscrutable jumbled message—apparently the idea was that Leibniz could have both unscrambled it (not likely) and gleaned its meaning (even less likely).

After this episode, the controversy cooled until Leibniz wrote a review of two of Newton’s works in 1705. In it, he compared Newton and himself to two other mathematicians. Leibniz probably just meant to say that he and Newton, like this other pair, had combined their ideas to come up with greater ideas. Another friend of Newton, however, pointed out that the analogy could be interpreted a different way: one of the two mathematicians Leibniz mentioned had probably plagiarized the other. Was Leibniz trying to say the same about himself and Newton?

COUNT ME IN!

Soon, this friend published a paper in which he cut right to the chase. He stated that Newton was the inventor “beyond any shadow of doubt” and that Leibniz had published it “having changed the name and symbolism.” This was too much for Leibniz. He wrote, enraged, to the Royal Society of London demanding an apology. Instead of an apology, he got a counterattack: a letter spelling out all of the claims against Leibniz in greater detail. Leibniz fired back another letter of protest.

The Royal Society’s response this time was to appoint a committee to investigate the matter. Unluckily for Leibniz, Newton (who was by now convinced that Leibniz stole calculus from him) was the president of the Royal Society at the time. Newton was not officially a member of the committee, but the report came out suspiciously strongly in his favor. Rather more suspiciously, the report was written in his handwriting. It stated firmly that Newton had been the first discoverer of calculus, and that Leibniz had plagiarized it.

For Leibniz and his friends, this was the last straw. They accumulated more evidence against Newton and published a leaflet making their own case. It was published anonymously (the author was given as a “leading mathematician”), but the question of who wrote it didn’t remain open very long. Now both Newton and Leibniz believed unshakably that the other was a dirty rotten thief.

CAN’T WE ALL JUST GET ALONG?

From there, the argument deteriorated into petty personal attacks and rehashings of the evidence already published. Even after Leibniz died the squabble continued. It wasn’t definitively established for the historical record that Newton and Leibniz were actually coinventors of calculus until the 20th century. We now know for certain that Newton came up with the basics of calculus in 1665–66 and Leibniz in 1675–76, before any communication between the two of them.

SUMMING UP

The final reckoning offers a nice compromise in the dispute. Newton was certainly the first one to hit upon the main ideas of calculus, beating Leibniz to it by about ten years. Leibniz, though, in being first to publish, received the honor of having his notation become the standard for the field—most of his symbols are still used today. And ironically, they both became known for all time as coinventors of calculus precisely from the notoriety of the dispute itself.