A Brief History of Pi
That the ratio of the circumference of a circle to its diameter is constant has been known to humanity since ancient times; yet, even today, despite 2000 years of thought, theories, calculations and proofs, π’s precise value remains elusive.
Ancient Civilizations
Babylonian
By the 17th century B.C., the Babylonians had a relatively advanced knowledge of mathematics, that they memorialized into complicated tables that expressed squares, fractions, square and cube roots, reciprocal pairs and even algebraic, linear and quadratic equations.
It should come as no surprise, then, that these math whizzes had also discerned an estimate of π at:
![]() This is pretty good, considering they were counting on their fingers – one theory for the development of Babylonian mathematics, which worked on a base 60 numeric system, was that they used the 12 knuckles of the fingers (not counting the thumb) multiplied by the five fingers of the other hand. Nifty.
This is pretty good, considering they were counting on their fingers – one theory for the development of Babylonian mathematics, which worked on a base 60 numeric system, was that they used the 12 knuckles of the fingers (not counting the thumb) multiplied by the five fingers of the other hand. Nifty.
Egyptian
Contemporaneous with the Babylonians, the Egyptians were also making great strides with mathematics, and are believed to have developed the first full-fledged base 10 number system.
The oldest evidence of π in Egypt is found in the Rhind Papyrus, which dates from about 1650 B.C. Together with instructions for multiplication and division, and evidence of prime numbers, fractions and even some linear equations, the Egyptian π was calculated as
When the Hebrews were building the Temple of Solomon around 950 B.C., they recorded its specifications, including that of a large brass casting as described in I Kings 7:23: “Then he made the molten sea; it was made with a circular rim, and measured 10 cubits across, five in height and thirty in circumference.”
Note that the ratio between the circumference and the diameter is 3. Not terribly precise, but also not bad, considering they had only emerged from the wilderness a few centuries before.
Greek
The Greeks greatly advanced the study of mathematics, and particularly the field of geometry. One of their earliest quests, dating back to at least the 5th century B.C., was to “square the circle” – create a square with exactly the same area as a circle. Although many tried, none were quite able to accomplish the feat, although the reason why was not explained for another 2000 years.
In any event, by the 3rd century B.C., Archimedes of Syracuse, the great engineer and inventor, devised the first known theoretical calculation of π as:
![]() At this point, Archimedes’ calculation is around 3.1418, by far the closest approximation up to this point.
At this point, Archimedes’ calculation is around 3.1418, by far the closest approximation up to this point.
About 400 years later, another Greek, Ptolemy, further refined the estimate of π using the chords of a circle with a 360-sided polygon to obtain:
Dating back to 2000 B.C. and built on a 10 based, place value system, Chinese mathematics were well developed by the 3rd century A.D. when Liu Hiu, who also developed a type of early calculus, created an algorithm to calculate π to five correct decimal places.
Two-hundred years later, Zu Chongzhi calculated to six decimal places, and demonstrated the following:
Middle Ages
Persian
Working in the 9th century A.D., Muhammad Al-Khwarizmi, widely credited with creating two of algebra’s most fundamental methods (balancing and reducing), the adoption of the Hindu numbering system (1-9, with the addition of a 0) and the inspiration for the words algebra and algorithm, is said to have calculated π accurately to four decimal places.
Several hundred years later, in the 15th century A.D., Jamshid al-Kashiintroduced his Treatise on the Circumference in which he calculated 2 π to 16 decimal places.
Modern Era
Europeans
From al-Kashi’s time through to the 18th century, developments related to pi generally were limited to producing ever more precise approximations. About 1600, Ludolph Van Ceulen calculated it to 35 decimal places, while in 1701, John Machin, who is credited with creating better methods for approximating π, was able to produce 100 digits.
In 1768, Johann Heinrich Lambert proved that pi is an irrational number, meaning it is a real number that cannot be written as a quotient of integers (recall Archimedes’ calculation, where π exists between two quotients of integers, but isn’t defined by one).
There was a π lull again, until finally, in the late 19th century, two more interesting things happened: in 1873, William Shanks correctly calculated pi to 527 places (he actually produced 707, but the last 180 were wrong), and in 1882, Carl Louis Ferdinand von Lindemann proved, in Über die Zahl, that π is transcendental, meaning:
Pi transcends the power of algebra to display it in its totality. It can’t be expressed in any finite series of arithmetical or algebraic operations. Using a fixed-size font, it can’t be written on a piece of paper as big as the universe.
Because he proved pi’s transcendence, Lindemann also proved, once and for all, that there was no way one could “square the circle.”
Americans (well, Hoosiers)
In the 19th century, not everyone kept up on the latest in the world of mathematics. This must have been the case with Indiana amateur mathematician Edwin J. Goodwin. In 1896, he had so convinced himself that he had, in fact, found a way to “square the circle,” that he talked a representative of the Indiana House into introducing a bill (to become a law) that his value of pi was correct.
Luckily, before the Indiana legislature got too far down that road, a visiting Purdue University professor informed the esteemed body that it was impossible to square the circle, and, in fact, Goodwin’s “proof” was based on two errors, most pertinent to this article, the error that
![]() Cooler heads in the Senate prevailed, and the bill was set aside with one Senator remarking that, in any event, their legislative powers did not extend to defining mathematical truths.
Cooler heads in the Senate prevailed, and the bill was set aside with one Senator remarking that, in any event, their legislative powers did not extend to defining mathematical truths.
If you liked this article, you might also enjoy our new popular podcast, The BrainFood Show (iTunes, Spotify, Google Play Music, Feed), as well as:
- The Truth About Einstein and Whether He Failed at Mathematics as a Child
- The Horse that Could Do Math: The Unintentional Clever Hans Hoax
- “Math” vs. “Maths” and Why Mathematics has an ‘S’ on the End
- Honey Bees Know the World is Round and Can Calculate Angles
- How to Quickly and Easily Tell if a Number is Divisible by 11, and Other Math Tricks
Bonus Fact:
- The mathematical volume of a pizza is pizza. How does that work you say? Well if z = radius of the pizza and a = the height then Π * radius2 * height = Pi * z * z * a = Pizza.
- 15 Most Famous Transcendental Numbers
- Al-Kashi
- Chinese Mathematics
- Egyptian Mathematics
- Greek Mathematics
- A History of Pi
- The History of the Indiana Pi Bill
- Islamic Mathematics
- I Kings, chapter 7
- Johann Heinrich Lambert
- Carl Louis Ferdinand von Lindemann
- Pi Day: History of Pi (Exploratorium)
- Ptolemy
- Sumerian/Babylonian Mathematics
- Zu Chongzhi
| Share the Knowledge! |
|


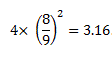




Not one of Indiana’s proudest moments. Can we just forget this ever happened and move on? Huh?
2 for the road
——————-
Fibonacci sequence – 1 1 2 3 5 8 13 21 34 55 89 144 ……. v 1.618
The Fibonacci sequence is named after Fibonacci. His 1202 book Liber Abaci introduced the sequence to Western European mathematics, although the sequence had been described earlier in Indian mathematics. By modern convention, the sequence begins either with F0 = 0 or with F1 = 1. The Liber Abaci began the sequence with F1 = 1, without an initial 0.
Fibonacci numbers are closely related to Lucas numbers in that they are a complementary pair of Lucas sequences. They are intimately connected with the golden ratio; for example, the closest rational approximations to the ratio are 2/1, 3/2, 5/3, 8/5, … . Applications include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings,[such as branching in trees, phyllotaxis (the arrangement of leaves on a stem), the fruit sprouts of a pineapple, the flowering of artichoke, an uncurling fern and the arrangement of a pine cone.
Origins
The Fibonacci sequence appears in Indian mathematics, in connection with Sanskrit prosody. In the Sanskrit oral tradition, there was much emphasis on how long (L) syllables mix with the short (S), and counting the different patterns of L and S within a given fixed length results in the Fibonacci numbers; the number of patterns that are m short syllables long is the Fibonacci number Fm + 1.
Susantha Goonatilake writes that the development of the Fibonacci sequence “is attributed in part to Pingala (200 BC), later being associated with Virahanka (c. 700 AD), Gopāla (c. 1135), and Hemachandra (c. 1150)”. Parmanand Singh cites Pingala’s cryptic formula misrau cha (“the two are mixed”) and cites scholars who interpret it in context as saying that the cases for m beats (Fm+1) is obtained by adding a [S] to Fm cases and [L] to the Fm−1 cases. He dates Pingala before 450 BC.
–
Redshift increases with distance
——————————————–
The law states that the greater the distance between any two galaxies, the greater their relative speed of separation.
This discovery was the first observational support for the Big Bang theory which had been proposed by Georges Lemaître in 1927 – a Belgian Roman Catholic priest, astronomer and professor of physics at the Université catholique de Louvain.
Earlier, in 1917, Albert Einstein had found that his newly developed theory of general relativity indicated that the universe must be either expanding or contracting. Unable to believe what his own equations were telling him, Einstein introduced a cosmological constant (a “fudge factor”) to the equations to avoid this “problem”.
In the 1930s, Hubble was involved in determining the distribution of galaxies and spatial curvature. These data seemed to indicate that the universe was flat and homogeneous, but there was a deviation from flatness at large redshifts.
When Einstein learned of Hubble’s redshifts, he immediately realized that the expansion predicted by General Relativity must be real, and in later life he said that changing his equations was “the biggest blunder of [his] life.”
In fact, Einstein apparently once visited Hubble and tried to convince him that the universe was expanding.
The Higgs boson is named after Peter Higgs, one of six physicists who, in 1964, proposed the mechanism that suggested the existence of such a particle. Although Higgs’s name has come to be associated with this theory, several researchers between about 1960 and 1972 each independently developed different parts of it.
In mainstream media the Higgs boson has often been called the “God particle”, from a 1993 book on the topic; the nickname is strongly disliked by many physicists, including Higgs, who regard it as inappropriate sensationalism.
In 2013 Peter Higgs and François Englert were awarded the Nobel Prize in Physics for their discovery.
Other references:
———————-
Stephen William Hawking – born 8 January 1942
The Higgs boson or Higgs particle
Edwin Powell Hubble (November 20, 1889 – September 28, 1953)
The Hubble Space Telescope (HST)
Kepler is a space observatory launched by NASA
The James Webb Space Telescope (JWST)
The European Organization for Nuclear Research – known as CERN
The International Space Station (ISS)
– Wikipedia, the free encyclopedia
52
——
Fifty-two is the 6th Bell number and a decagonal number. It is an untouchable number, since it is never the sum of proper divisors of any number, and it is a noncototient since it is never the answer to the equation x – φ(x).
The first few untouchable numbers are:
2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, 290, … (sequence A005114 in OEIS)
The number 5 is believed to be the only odd untouchable number, but this has not been proven: it would follow from a slightly stronger version of the Goldbach conjecture. Thus it appears that besides 2 and 5, all untouchable numbers are composite numbers. No perfect number is untouchable, since, at the very least, it can be expressed as the sum of its own proper divisors.
There are infinitely many untouchable numbers, a fact that was proven by Paul Erdős.
– Wikipedia, the free encyclopedia